BACK TO HOME →

STRUCTURAL HIGH CYCLE CREEP-DAMAGE PROCESSES

BRESLAVSKY D., MORACHKOVSKY O.,

National Technical University «Kharkiv Polytechnic Institute»,

21 Frunze Str., Kharkiv, 61002, Ukraine

e-mail: brdm@kpi.kharkov.ua

The paper is devoted to theoretical foundations and method of simulation for cyclic creep-damage processes in structural members. The basic equations were derived by use of the method of asymptotical expansions on small parameter as well as the method of averaging on the period of a stress cycle. The cyclic creep-damage constitutive equations, which were derived by the authors, are given. The possibilities of the method are illustrated by examples of numerical calculations of turbine blades.

1. Background and significance. The behaviour of materials in structures under elevated temperatures is essentially time-dependent. Large amount of structural members are working under variable, cyclic loading. The phenomenon of ‘creep-fatigue interaction’ is well known and investigated for the case of low-cycle fatigue. At the same time the working conditions of different engineering objects, such as gas-turbine engines, supersonic planes etc. are characterized by significant frequencies of external oscillation action (more than 1..3 Hz). The number of cycles to fracture in that case is more than 50000-100000. In conditions of joint action of static and cyclically varying stress fields the cyclic creep strains are developed in solids. Usually they are accompanied by damage accumulation processes, which are lead to fracture.

The paper is devoted to the presentation of mathematical models and constitutive equations for creep-high cycle fatigue interaction processes in solids.

2. Problem statement. Let us regard the solid with volume V, fixed on the surface part S₁ and loaded by traction р on another surface part S₂=S₃ÈS₄. The material points continuum’s motion in co-ordinate system x=(x₁,x₂,x₃) will be described by Lagrange approach by vectors of displacements u and their rates v, by stress s_ij=s_ji and strain e_ij=e_ji (і,j=1,2,3) tenzors, which are the functions of co-ordinates and time t. Creep irreversible strains without consideration of their influence on compression will be described by tenzor c_ij=c_ji . Used constitutive equations define the tenzorial connection between the creep strain and stress tenzors and time. Let us refine the character of external loading field. The external forces will be divided on two components, which are the basic and the oscillatory actions. The first one includes the volume forces f(x,t), xÎV, and the traction part р⁰(x,t), xÎS₃ , which is slowly varying in time or remains constant.

The oscillatory field of external loading, which is acted on S₄ (in particular case it can be S₄ÎS₃), is regarded as polyharmonic with components

, (1)

where p^r_i, p^q_i are the amplitudes of traction components, which correspond for harmonics with index ‘г’ or ‘q’; R_i, Q_i are the numbers of harmonics.

The Ф_і(t) are the periodic polyharmonic functions with period, such as , where t_* is time to creep fracture.

Mathematical problem statement for boundary – initial value creep problem for cyclically loaded solids by use the formulated assumptions can be presented by following system of equations:

; (2)

, ,

where r is the mass density, n – the normal unit for solid boundary, і=1,2,3; С_ijkl is the tenzor of material elastic properties; `u_i are the known values of surface S₁ points displacements, which are constant in time.

The system (2) is substantially nonlinear. It is connected with nonlinear correlations between creep strain tenzor c_ij and stress tenzor s_ij. The definite form of constitutive equations is discussed below. The nonlinear geometric relations with small strains and shears will be considered.

From the mathematical point of view, the considered problem is referred to the system of differential equations for the motion of a solid under the action of static and cyclic external loading. Creep analysis using a class of implicit single step algorithms is not possible in this case because the large number of small time steps usually required for accurate solution could not be successfully extended to dynamic problems.

Due to the fact that period of oscillatory action T is much more smaller than period of basic motion t_* ,the asymptotical expansions (AE) on the small parameter with coefficients, which are dependent upon both variable t (slow or macroscopic motion) and variable t=t/m or x= t/T (fast or microscopic motion) for the unknowns of system (2) can be written:

. (3)

Here under z the arbitrary unknown of system (2) can be considered; x, t, and x can be considered formally as independent variables. zⁱ is one-periodic function of x (0 £ x £ 1) ,and its averaged on the period values are equal to zero:

ázⁱ(x,t,x)ñ= (4)

As usual, we can write for time derivative:

. (5)

Let us save only two terms in each of asymptotic expansions (3):

. (6)

For example, for displacements and stress we have:

;. (7)

With consideration of (5) the following expression can be obtained for displacements rates:

, (8)

where , .

For strain rate components we have:

. (9)

Due to the fact that penultimate term in (9) has the m² as a multiplayer and due to regarded small vibrations, we can neglect the considered penultimate term. The analysis of underlined term shows, that it is infinitely small in comparison with another terms and we can neglect this term too. Then, by signing

; (10)

,

we obtain the expression for strain tenzor

. (11)

Let us mark, that in equations (7) - (11) the coefficients of the m depend not only upon t or x, but upon co-ordinates х too.

Than derived equations (7) - (11) can be substitute to the basic system (2), which determines the solid motion in the case of cyclic creep.

Further the obtained equations can be averaged on the period of oscillations. For example, for equilibrium equations we have:

(12)

For the physical equations:

, (13)

and so on. The average values of coefficients are equal to themselves, <z¹>=0 due to (4).

The asymptotical expressions and averaging on the period allows to divide the initial system (2) on two ones: the first system appears from relations are left after averaging on the period of oscillations, and describes the processes which take place in slow basic motion:

(14)

, ,

Here all unknowns are the functions which are slowly varied in time scale t. Inertial term in (14) are formally followed from derived equations, but in practical calculations it have to be neglected.

The second system can be obtained by subtraction the (2) and (14):

(15)

; , , 0<x<1

In this system all unknowns are varied in fast time scale x.

The system (15) is linear. With accuracy of multiplayer 1/m² it corresponds to the problem of small elastic forced vibrations. So, the solution of this system can be found as a superposition of harmonic functions, which are varying with frequencies 2prm [2]. The solution can be obtained by division the variables on co-ordinates and time:

(r=1,R) , (q=1,Q). (16)

After usual transformations, the system of equations for the boundary problem for amplitude values of ‘q’ harmonic of ‘fast’ unknowns takes the following form:

, ;

,; (17)

Similar system can be written for the ‘r’th harmonic. So, we have the solution of the system (15)

.

as a sum of the solutions for each r and q. As usual, for stresses we can obtain:

(18)

In the case of one-periodic harmonic loading, when, for example, R=0, Q=1, we have the harmonic process with the frequency of forced vibrations W=2p/T.

When we can consider not both infinitesimal strains, and infinitesimal angles of rotations, as it can be observed in many cases, the geometric relations in (14) are linearized and take the form:

(19)

Two obtained systems (the first one for basic motion in creep-damage process and the second system describing the forced oscillations) are not independent. As were found by different experimental observations [3], the stress values (18) are obtained after solution of system (15), have to be included to the flow rule and the damage evolution equation.

3. Constitutive equations. Now let us present new cyclic creep-damage constitutive equations with consideration of damage due to creep and high-cycle fatigue.

The concept of rational mechanics was used. Following it, the description of the material evolution due to the cyclic loading will be done by such observable variables as full strain tenzor e=e^e+c and temperature Т, by internal variables such as creep strain deviator and structural parameters; and associated variables such as stress tenzor s, entropy and thermodynamic forces.

So-called high-cyclic processes of loading were considered. In that case the time to fracture value is equal to t_*=N_*/f, where f is the frequency of the cyclic loading, and the number of stress cycles in a material point is more than N_*=(0.5..1)×10⁵. In considered conditions the relation between the cyclic stress period Т=1/f and time to fracture is a small parameter which is less than 1:

. (20)

The processes of high-cycle fatigue and so-called ‘dynamic creep’ processes [3] are corresponded to conditions (20).

Used creep constitutive equations are :

(21)

and

(22)

with damage w evolution equation:

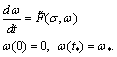(23)

The equations (21)-(23) are used for description of the cyclic creep processes using the method of asymptotical expansions of all variables on small parameter m with coefficients, which depend upon both t (‘slow’ motion with index’0’) and t= t/m or x= t/T (‘fast‘ motion with index ‘1’).

Simple cyclic loading, when all stress deviator’s components are varied by the same ways in the 5D stress space, is considered.

The asymptotic expansion of stress tenzor has the form (7). Two terms are retained here. Fast varying stress component has the following presentation:

, (24)

where s^r, s^q – are amplitude values of harmonics, R, Q are the numbers of harmonics.

By use the asymptotic expansions and the averaging in a period technique for the equations (21)-(23) the equations for description of high cyclic creep-damage processes are obtained.

In the case of one harmonic loading and power creep law the approximate analytical expressions for dynamic (A<A_cr) creep rate with consideration of damage evolution were obtained: For example, for Norton creep-damage law we have:

; (25)

, (26)

where s_vМ, s_eq – are von Mises stress and equivalent stress in three invariants criterion; are the stress cycle asymmetry parameters; H(A)=G(A;n), K()=G(;m);; B, D, n, m, l – are the material constants.

The relation, which was built using the widespread hypothesis of the different kinds of damage accumulation [4], was used for general high cyclic creep-damage evolution equation. The functions a_f() and b_f() allow to represent the income of both damage mechanisms (creep w_с and high cycle fatigue w_f) into the accumulated damage. At the same time those functions can be regarded as a probabilities of transitions to fracture due to creep or high cycle fatigue mechanisms.

The use of applicable invariants for the damage description at the case of complex stress state is discussed. The equivalent stress from three invariants criterion is used for creep damage; high-temperature high cyclic fatigue damage is described using the Sines criterion by equivalent stress c_f. The forms of influence functions a_f() and b_f() were chosen due to experimental data.

For example, let us present the more frequently used form of constitutive equations:

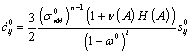; (27)

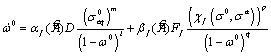w⁰(0) = 0, w⁰(t_*) = 1, (28)

where s⁰_ij is the stress deviator components are varied in ‘slow’ time.

The material constants B, D, n, m, l, F_f, p, q and functions a_f, b_f are included in (27)-(28) have to be determined by creep-fatigue experiments. The suggested equations were built using the criterion of the minimum number of these constants. In general case this number is equal to 14. The basic experiments, which have to be provided in order to determine these constants, were selected. All of them are standard for the creep and fatigue theories. The additional experiment is cyclic creep testing with the different levels of stress cycle asymmetry parameter.

The thermodynamic justification of the above equations has been done and their agreement with the fundamental laws of solid mechanics has been verified.

The presented high cyclic creep-damage equations were verified by use of known experimental data. Cyclic creep curves, long-term strength curves, limit strain curves for more than twenty high-temperature steels and nickel-based alloys were used for the verification.

These experiments show rather high power of accuracy. The maximum error in cyclic creep description is equal to 25-30%, for creep damage parameters is equal to 15-25%, for fatigue damage parameters is equal to 25-30%. Obtained accuracy allows to recommend the derived cyclic creep-damage equations for the long-term strength estimations.

The systems of equations (14), (15) are added by the physical relations (27) – (28) determine the mathematical problem of high cyclic creep-damage at the complex stress state.

The FEM algorithms using for the numerical simulation are discussed in [5], [6].

4. Numerical example. Let us present the results of numerical investigations of turbine blades using the calculation scheme of short plane plates. The creep process in blades loaded by centrifugal forces and normal pressure with harmonic law (in case 1 the frequency is 100 Hz, in case 2 the frequency is 1100 Hz) were studied. The materials are high temperature nickel-based alloys EI867 and EP109 at temperature 1173К.

Triangular plane elements were used. The analysis of eigen value problem shown that cases 1 and 2 correspond to the plate’s motion due to first and second forms of forced bending vibrations.

Figure 1 demonstrates the levels of damage parameter w at the blade surface (alloy EI867) before the fracture moment at cases 1 (left) and 2 (right). The results show that the area near the maximum damage value is corresponded to the area in which the macrocracks can initiate according to the experimental data.

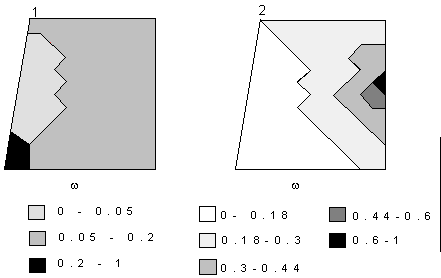
Figure 1. Damage parameter distribution in the blades

The temperature fluctuations in nuclear reactors lead to the repeated deformation of the shell surface in heat assemblies. This one causes the high frequency loading. The problem is regarded with the purpose of evaluation the stress-strain state and the creep damage accumulation. The calculational scheme of the heating element is the cylindrical shell made from high-temperature type 316 L steel. The temperature is equal to 873К. The internal pressure is varied due to the following law: p=p⁰+p^a×sin2pft×cos3j, where j is the angle co-ordinate, p⁰, p^a are the constant and the amplitude pressure components.

The four node finite element of the shell of revolution with 28 degrees of freedom was used for the numerical simulations. The results (figure 2) were obtained for cyclic (curve 1, L= p^a/p⁰ =0.05) and static creep under the pressure p⁰=65МПа (curve 2). The analysis of the numerical data shows, that the symmetric character of deformation was lost due to cyclic creep. The reason of this nonaxisymmetric strain accumulation is the substantial angle irregularity of the pressure. 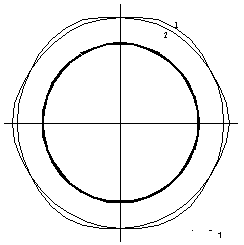After the first year at the working conditions the important shape changes can be observed (figure 2, a). Here the initial shell geometry is drawn by the bold line (the scale 1 is equal to 1 mm); curves 1 and 2 show the static and cyclic creep deflections.

The relaxation of the maximum stresses is caused the nonaxisymmetric stress redistribution (figure 2,b). Here the curve’0’ is marked the initial level of axial force N₁ at t=0.

The results show, that cyclic variation of the pressure has to be added to the usual limit factors, such as elevated temperatures, pressure and irradiation effects. The lost of shell shape can be the first reason of fracture in this case.

a b

Figure 2. Variation of the shell shape and axial forces in the central cross section

5. Conclusions. The method for the cyclic creep-damage problem solution, which is based on the procedures of asymptotic expansions and averaging in the period of the solid’s forced vibrations, is presented here. This mathematical technique leads to some ‘homogenisation’ of the cyclic creep-fatigue process.

The obtained numerical results show, that the properties of cyclic creep strain and damage accumulation in 2d objects are the decreasing of the lifetime and the increasing of creep strain rate in comparison with pure static loading.

References: 1. Breslavsky D., Morachkovsky O. A new model of nonlinear dynamic creep// IUTAM Symposium on Anisotropy, Inhomogenity and Nonlinearity in Solid Mechanics.- Dordrecht: Kluwer Academic Publishers. - 1995. - P. 161-166. 2. Warburton G.B. The dynamical behaviour of structures. Oxford et al: Pergamon Press, 1976. 3.Rabotnov Yu.N. Creep problems in structural members. – Amsterdam: North Holland, 1969. 4. Lemaitre J., J.-L.Chaboche. Mechanics of solid materials. - Cambridge: University press, 1994. 5. Breslavsky D., Morachkovsky O. Dynamic creep continuum damage mechanics: FEM-based design analysis// Computational Plasticity: Fundamentals and Applications. Proc. of the Fifth International Conference on Computational Plasticity held in Barselona, Spain, 17-20 March 1997. - Barselona :IMNE. - 1997. - Part 1. - P.1071-1076. 6. Altenbach H., Breslavsky D., Morachkovsky O., Naumenko K. Cyclic Creep-Damage in Thin-Walled Structures// Journal of Strain Analysis for Engineering Design. 2000, Vol.35, No 1. –p.p. 1-11.