Linear and forced nonlinear vibrations of shallow shells with two simply
supported and two free edges
Summary. The exact eigenmodes of shallow
shells with simply supported opposite edges is obtained. Eigenmodes of linear vibrations of shallow
shell with two simply supported and two free edges are treated. The vibrations
of shallow shells with geometrical nonlinearity in the case of an internal
resonance are described by two-degrees-of-freedom system with essential
nonlinearity. The interaction of two shell modes is described by this system. The
harmonic balance method is used to study this system. The stability of shell periodic
motions is analyzed. The shallow shell bifurcation behaviour is analyzed;
symmetry-breaking and saddle- node bifurcations are observed.
1 Introduction
Shallow shells are elements of turbines, aircrafts and marine structures.
Significant dynamical loads frequently acts on these structures, which can lead
to their failure. Shallow shells perform lateral vibrations with amplitudes,
which are commensurable with the shell thickness. Then the shells motions are
described using geometrically nonlinear theory. Many efforts were made to study
vibrations of shallow shells with geometrical nonlinearity. Grigolyuk [1] investigated the
vibrations with moderate amplitudes of simply supported panel using two-mode expansion.
Cummings [2] considered the
vibrations of simply supported
cylindrical panel under the action of impacts loads. Using single-mode approximation,
Leissa and Kadi [3] investigated
nonlinear free vibrations of simply supported shallow panel with different values
of the principal curvatures in two orthogonal directions. The nonlinear
vibrations of simply supported cylindrical panel are analyzed by Vol’mir,
Logvinskaya, Rogalevich [4]. Three and five degrees-of-freedom
models are treated. Free vibrations of clamped cylindrical panels are analyzed
in the paper [5]. The spline finite strip method is developed to analyze free
vibrations of doubly curved shallow shells with rectangular base in [6, 7]. Liew and Lim [8] analyzed linear free vibrations of rectangular base shallow shells with different curvatures and different
boundary conditions. The middle thickness shallow shells are analyzed
accounting shear by Liew, Lim [9]. Baumgarten and Kreuzer [10] analyzed
two- and four-modes models of cylindrical panel nonlinear vibrations. Yamaguchi and Nagai [11] investigated chaotic vibrations of square base shallow
shells with flexible edges using finite degrees-of-freedom shell model. Awrejcewicz and Krysko [12] analyze
the period-doubling bifurcations and chaotic motions of rectangular plate. The forced
vibrations with moderate amplitudes of doubly curved panels with rectangular
base in the case of the internal resonance are considered in [13].
Nonlinear vibrations of shallow shells with complex boundaries are treated in
[14, 15]. The influence of the initial imperfections on the nonlinear vibrations of
shallow shells is analyzed by Amabili [16-18]. The exact eigenmodes of the rectangular plate
with two simply supported opposite edges are obtained in [19]. The similar
expressions for open cylindrical shells are derived in [20]. Free vibrations of
Levy- type thick functionally graded cylindrical shell panels are investigated
to identify the validity range of Donnell and Sanders theories in [21]. Free
vibrations of two-dimensional functionally graded open cylindrical shell are
analyzed using 2-D generalized differential quadrature method in [22]. Nonlinear
modes of simply supported cylindrical shell are treated in [23].
Free and forced
vibrations of shallow cylindrical panel, which is simply supported at the opposite
edges and free at others edges, are analyzed. The exact eigenmodes of shallow
shells with simply supported opposite edges are obtained. The effect of the
shell parameters on the eigenfrequencies and eigenmodes is analyzed. It is
shown that the first eigenfrequency does not depend on both the shell curvature
and the length along simply supported edges. If the length along the simply
supported edges is increased, the higher eigenfrequencies are decreased. The
shell nonlinear vibrations with moderate amplitudes in the case of internal
resonance are considered. Due to this internal resonance two eigenmodes of
shell vibrations are interacted. In order to study this interaction essentially
nonlinear two-degree-of-freedom system is obtained and analyzed by using the harmonic
balance method. As a result of stability analysis, saddle-node and a
symmetry-breaking bifurcation are analyzed.
2 Problem formulation
The forced nonlinear
vibrations of simply supported shallow shell with rectangular base (Fig. 1)
under the action of the concentrated force are considered. The double curved
shallow shell is analyzed. As thin shell is treated, shear and rotation inertia
are not taken into account. It is assumed, that the shell displacements are
moderate; stresses and strains are small. Then stresses and strains satisfy the
Hooke’s law; strains and displacements are connected by nonlinear relations. Then
the Donnell equations with respect to the displacements are used [24, 25]:
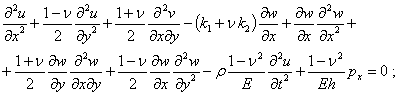(1)
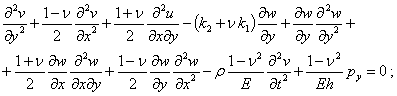(2)
|
|
(3) |
where 
are displacements of the shell middle surface in 
directions, respectively; 
,
are Young’s modulus, Poisson’s ratio
and material density; 
and 
are curvatures of shell middle surface in x and y directions, respectively; 
is the shell thickness; 
are intensities of the external forces.
The
edges 
; 
are simply supported and the edges 
; 
are free. Then the following boundary
conditions are satisfied:
; 
; 
; 
; (4)
; 
; 
; 
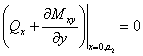, (5)
where 
, 
, 
are membrane forces per unit length; 
, 
, 
are moments per unit length; 
are transverse shear forces [24]:
; 
;
;
.
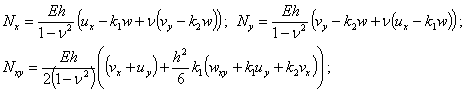
3 Free linear vibrations of shell
Nonlinear vibrations are expanded into the truncated series by eigenmodes.
Therefore, before analysis of nonlinear problem, the shell eigenmodes are calculated.
Then the nonlinear terms are not taken into account in
the equations (1-3) and it is assumed that 
. In future analysis it is considered
the doubly curved shallow shells with arbitrary boundary conditions at the edges ; . The
boundary conditions (4) satisfy at the edges and .
Using the separation of
variables and satisfying the boundary condition (4), the shell vibrations are
presented as:
;
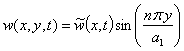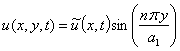; (6)
,
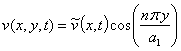where 
is positive integer.
The
shell displacements (6) are substituted into the linearized Donnell equations
(1-3). As a result, the following system of partial differential equations with
respect to 
is derived:
(7)
(8)
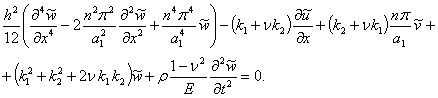(9)
The displacements 
are presented in the following form:
; 
; 
. (10)
The solution (10) is substituted
into (7-9). As a result, the system of ordinary differential equations with
respect to 
is obtained. The
solution of this system takes the following form:
; 
; 
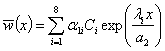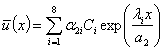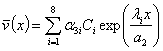, (11)
where 
are constants of
integration. The displacements
;
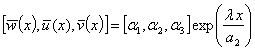are substituted into (7-9) to obtain
the parameters 
,
. As a
result, the system of linear algebraic equations with respect to 
is derived:
(12)
The elements of the matrix 
are the following:
;
; 
;
; 
; 
;
; 
; 
.
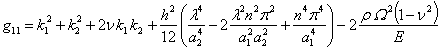The determinant of the system (12) is
equated to zero and the following characteristic equation with respect to 
is derived:
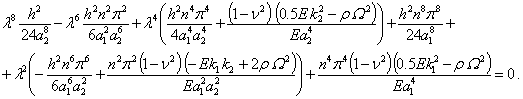(13)
One element of the eigenvector 
is taken equal to 1: 
. We stress, that the values 
and 
are complex.
The
solutions (6, 10) are substituted into the boundary
conditions (5). After the variables separation the following boundary
conditions are derived:
|
|
(14) |
;
; 
;
.If the solutions (11) are
substituted into the equations (14), the homogeneous system of eight linear
algebraic equations with respect to is obtained.
The solution of the equation (13) corresponding
to the first eigenfrequency 
are the following:
(15)
where 
are numbers, which are
obtained from the numerical solution of equation (13). The solutions of the
equation (13) for higher eigenfrequencies take the form:
.
For
the first eigenfrequency the eigenmodes of the lateral
displacements takes the form (A.1) from Appendix. The eigenmodes 
and 
takes the form (A.2)
from Appendix.
The
solutions (A.1) and (A.2) are substituted into the boundary conditions (14). As
a result the system of linear algebraic equations with respect to is obtained. The
frequency equation with respect to 
is obtained by equating to zero the
determinant of this system. The parameters are obtained from the system of linear
algebraic equations. Using the above-considered approach, the exact analytical
form of eigenmodes is derived. These eigenmodes are presented in Appendix.
The suggested approach differs from the
method [24], where the last boundary condition (4) is not taken into account. We stress that the eigenmodes (6, 10, 11) satisfy all
boundary conditions at the edges and .
4 Numerical analysis of linear vibrations
The steel shallow shell
with the following parameters: 
N/m2, 
kg/m3, 
, a1=1 m, a2=0.6 m, h=0,01 m, 
m is analyzed. The
edges 
and 
satisfy the boundary conditions (5). Table 1
shows the results of eigenfrequencies calculations. The eigenfrequencies of the plates, which are obtained using the
relations from [20, 26], are presented in the first row. Table 2 shows the dependence
of the eigenfrequencies on the shell length at a1=1 m, 
m, h=0.01 m. For all
considered parameters of the shell the eigenmode of the first eigenfrequency (
) have no nodal lines parallel to 
axis. The eigenmodes
of the second and the third eigenfrequencies have one and two nodal lines
parallel to ó axis, respectively. As follows from Tables 1, 2, the frequencies of the eigenmodes
without nodal lines parallel to ó axis do
not depend on the shell geometrical parameters; the frequencies of the eigenmodes
with one nodal line parallel to ó axis do
not depend on shell middle surface curvature.
The eigenfrequencies of
the shallow shell are determined by the Rayleigh-Ritz method to verify the
obtained results. The trial functions are used for the expansions of 
, which
satisfying the boundary
conditions (4). Table 3 shows the results of the eigenfrequency calculations for
the shells with the parameters a1=1 m, a2=0.7 m, 
m, h=0,01 m. As can be
seen from Tables 2 and 3, the eigenfrequencies, which are obtained by the
Rayleigh-Ritz method, are close to the eigenfrequencies, which are obtained
from analytical analysis.
As follows from Tables 1
and 2, internal resonances can occur in the shallow shells.
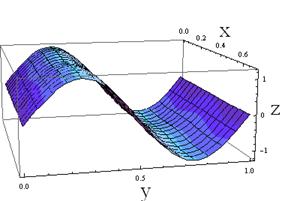
Fig. 2 shows three
eigenmodes of the shell linear vibrations with the following parameters: a1=1 m, a2=0.7 m, m, h=0.01 m. These eigenmodes correspond to the eigenfrequencies: 154.9; 324; 619.9 rad/s.
5 Nonlinear vibrations analysis
The forced vibrations of
the shell (Fig. 1) under the action of the point force are considered. This
point force has the following projections:
,
where 
is delta-function.
The shell displacements
fields are expanded by using the eigenmodes of linear vibrations [23, 14, 15]:
(16)
,
where 
are generalized
coordinates of the shell; 
are normalized vibrations eigenmodes, which are determined
in the previous section.
As
thin shells are considered, the eigenfrequencies of longitudinal vibrations are
significantly higher then the eigenfrequencies of bending vibrations. Therefore,
the displacements 
are significantly less than 
[23, 14, 15] and the inertial terms are not taken into account in the equations (1, 2). The
expansions (14) are substituted into the equations (1-3) and the Galerkin method
is used. Then the equation (3) is reduced to the system of 
ordinary differential equations. The system
of 2N linear algebraic equations with respect to 
is derived from the equations (1, 2). As a
result the following equations are obtained:
; (17)
; (18)
, (19)
where the parameters 
are obtained from the
numerical calculations. Solving the system of linear algebraic equations (20, 21),
the generalized coordinates 
are obtained as functions of
. These solutions are substituted into the system
of ordinary differential equations (19) and the -degrees-of-freedom model of the shell vibrations is
obtained.
The
following dimensionless generalized coordinates and dimensionless time
; 
;
are used.
It is assumed in future
analysis that the frequency of the external force is close to the first
eigenfrequency
, (20)
where 
is detuning parameter. As follows
from Tables 1, 2, the eigenfrequencies 
satisfy to the condition
of internal resonance:
, (21)
where 
is small parameter,
is detuning parameter.
It is assumed, that the
third and higher eigenfrequencies of the shell are significantly greater then 
. The frequency of the external force satisfies the equation
(20). The eigenfrequencies 
and meet the resonance
conditions (21). Then the third and higher vibrations eigenmodes can not be
accounted in the expansion for 
(16). The shell
vibrations are described by two-degree-of-freedom nonlinear dynamical system with
respect to the modal coordinates 
:
|
|
(22) |
The
harmonic balance method is used to study the vibrations of this system. The
shell vibrations are presented by the following truncated Fourier series:
. (23)
The solution (23) is substituted
into the dynamical system (22) and the coefficients at the same harmonics are
equated. Then the amplitudes 
satisfy the system of
nonlinear algebraic equations. This system can be presented in the following
general form:
(24)
The results of forced
vibrations analysis are shown on a frequency response. The continuation
technique [27] is used to obtain a frequency response. Then one of the
parameters from 
is preset with certain
step. The rest parameters are obtained by the solution of the system of
nonlinear algebraic equations (24).
The
stability of the motions 
is analyzed. Then
small perturbations 
are added to periodic
motions. Then small perturbations are described by the system of four linear
ordinary differential equations with respect to 
. This system can be presented in the following vector form:
(25)
where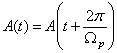 
is matrix with time
periodic elements. The fundamental matrix is calculated to estimate the periodic
motions stability [27, 28]. The fundamental matrix is solution of the system
(25). The identity matrix is used for initial conditions of the system (25):
The system of linear differential
equations with periodic coefficients (25) is solved four times to calculate the
fundamental matrix. This system is solved numerically by the Runge- Kutta
method. The multipliers, which are eigenvalues of the fundamental matrix, are
calculated. Stability of periodic solutions is estimated by using of the multipliers
[28, 29].
6 Numerical analysis of nonlinear vibrations
The numerical analysis
will be carried out for steel shell with the parameters:
a1=1 m, a2=0.7 m, 
, m, h=0.01
m, E=2.1∙1011
N/m2, ν=0.3.
The
Free
vibrations of the
system (22) are analyzed; thus 
. The vibrations modes with
active coordinate 
and 
are described by the following dynamical
system:
. (26)
The harmonic balance
method is used to study the dynamics of the system (26); the system motions are
presented as
(27)
The harmonic balance method is
applied to analyze the forced vibrations in Section 5. Then the solution (23)
contains the frequency of the external force 
. In this section the harmonic balance method is used to
analyze free nonlinear vibrations. In this case the solution (27) contains
unknown frequency 
.
The calculations with
sequential increase of the number of terms in the expansion (27) are carried
out to determine the sufficient number of terms to approximate nonlinear
vibrations. It is determined that four terms of the expansion (27) are enough
to approximate the vibrations. Fig. 3 shows by dot-and-dash line the
backbone curve for the vibrations amplitudes 
.
Free nonlinear
vibrations with two active coordinates 
and 
are observed in the system (22). Following the harmonic balance method, these motions are presented as:
, (28)
where is unknown frequency,
which is determined. The harmonic balance method considered in the previous
section is used. As a
result of these calculations, the motions, which are denoted by number 2 on
Figures 4, 5, are obtained. These vibrations have two active generalized
coordinates and 
. In this regime the harmonics with the amplitudes 
and 
dominate in the
solutions 
and 
, respectively.
Now the forced motions of the system
(22) are analyzed. It is assumed, that the external force with amplitude 
N is applied at the point 
. Then the parameters 
of the system (22) are: 
; 
. The parameters 
is equal to zero as the second eigenmode satisfy the equation 
. The harmonic balance method is
applied to the system (22).
The vibrations with 
and 
take place in the system
(22). These motions are described by the following equation:
. (29)
Performing numerical solution of the
system of nonlinear algebraic equations (24), two kinds of forced periodic vibrations
are obtained. The curves of these motions are denoted by the numbers 3 and 4 on
Fig. 3. Stable and unstable forced vibrations are shown by solid and
dotted curves on Figures 3-5. Curve 4 on Fig.3 shows the amplitude of the first harmonics 
. The harmonics
with the amplitude 
predominates in the vibrations, which are
described by the curve 3 on the left from the point A. The motions, which are described by the branch 3 (Fig. 3)
close to the point B, satisfy the symmetry
condition [30]:
, (30)
where Ò is
vibration period. The vibrations, which are described by
the curve 5 (Fig. 4, 5), are forked from the motions (30) due to the symmetry-breaking bifurcation [30]. This bifurcation behavior is determined on the basis of the numerical
calculations of the multipliers.
Now
the vibrations with two active coordinates 
are treated. These
motions are described by the curves 5, 6 on Figures 4, 5.
The harmonics with the amplitudes and 
predominate in the Fourier-series expansions of
the generalized coordinates and 
,
respectively. Note, that the harmonics with the amplitude 
contributes into the
Fourier-series expansion of .
The direct numerical
integration of the system (22) is carried out to verify the results, which are
obtained by the harmonic balance method. The initial conditions for the direct
numerical integration are chosen from the results, which are obtained by the
harmonic balance method. The results of the direct numerical integration are
shown by dots in Figures 3-5. Thus, the results of the harmonic balance method
and the data of the direct numerical integration are close.
7 Conclusions
The exact analytical expressions for the vibrations eigenmodes of
shallow shells with rectangular base and two simply supported edges are derived
in this paper. The connections between the eigenfrequencies of the panels and the
shell geometrical parameters are analyzed. It is shown that the first
eigenfrequencies do not depend on both the shell curvature and the length along
simply supported edges. If the length along the simply supported edges is
increased, the higher eigenfrequencies are decreased. We come to the conclusion
that the internal resonances can occur in such type of shallow shells.
Analysis
of free and forced nonlinear vibrations of shallow cylindrical panel accounting
internal resonances is performed. The backbone curves of shallow shells are
hard. The stability analysis of the periodic motions is carried out. The saddle-node
and symmetry-breaking bifurcations are observed in the shell.
Appendix
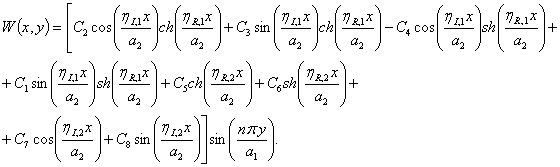(A.1)
The eigenmodes and are denoted by 
and 
, respectively. They can be presented as:
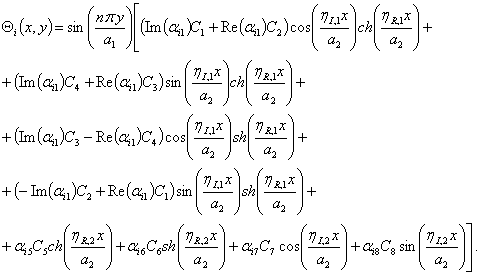(A.2)
Note, that the constants of
integrations are real.
References
[1] Grigolyuk,
E.I.: Vibrations of circular cylindrical panels subjected to finite deflection,
Prikl. Mat. Mekhanika 19, 376–382 (1955) (in Russian)
[2] Cummings,
B.E.: Large-amplitude vibration and response of curved panels, AIAA J. 2, 709–716 (1964).
[3] Leissa,
A.W., Kadi, A.S.: Curvature effects on shallow shell vibrations, J. Sound Vib. 16, 173–187 (1971).
[4] Vol’mir,
A.S., Logvinskaya, A.A., Rogalevich, V.V.: Nonlinear natural vibrations of
rectangular plates and cylindrical panels, Sov. Phys. Dokl. 17,
720–721 (1973).
[5] Srinivasan,
R.S., Bobby, W.: Free vibration of noncircular cylindrical shell panels, J. Sound Vib. 46, 43–49 (1976).
[6] Cheung,
Y.K., Li, W.Y., Tham, L.G.: Free vibration analysis of singly curved shell by
spline finite strip method, J. Sound Vib. 128, 411–422
(1980).
[7] Li, W.Y., Tham, L.G., Cheung, Y.K., Fan, S.C.: Free vibration analysis of doubly curved shells by spline finite strip method, J. Sound Vib. 140, 39–53 (1990).
[8] Liew, K.M., Lim, C.W.: Vibration of doubly-curved shallow
shells, Acta Mech. 114, 95–119
(1996).
[9] Liew, K.M., Lim,
C.W.: Vibration studies on moderately thick doubly-curved elliptic shallow shells, Acta Mech. 116, 83–96 (1996).
[10]
Baumgarten, R., Kreuzer, E.: Bifurcations and subharmonic resonances in
multi-degree-of-freedom panel's models, Mecc.
31, 309–322 (1996).
[11] Yamaguchi, T., Nagai, K.-I.: Chaotic vibrations of a cylindrical shell-panel with
an in-plane elastic-support at boundary, Nonlinear Dyn. 13, 259–277 (1997).
[12] Awrejcewicz, J., Krysko, V.A.: Feigenbaum scenario exhibited by thin plate dynamics,
Nonlinear Dyn. 24, 373–398 (2001).
[13]
Amabili, M.: Non-linear vibrations of doubly curved shallow shells, Int. J. Non-Linear Mech. 40, 683–710
(2005).
[14] Breslavsky I.D., Avramov, K.V.: Nonlinear modes
of cylindrical panels with complex boundaries. R-function method, Mecc. 46, 817-832 (2011).
[15]
Breslavsky, I.D., Strel’nikova, E.A., Avramov, K.V.: Dynamics of shallow shells
with geometrical nonlinearity interacting with fluid, Comput. Struct. 89, 496–506 (2011).
[16]
Amabili, M.: Nonlinear vibrations of circular cylindrical panels, J. Sound Vib. 281, 509–535 (2005).
[17]
Amabili, M.: Theory and experiments for large-amplitude vibrations of circular
cylindrical panels with geometric imperfections, J. Sound Vib. 298, 43–72 (2006).
[18]
Amabili, M.: Nonlinear Vibrations and Stability
of Shells and Plates,
[19] Leissa, A.W.: The free vibration
of rectangular plates, J. Sound Vib. 31, 257–293 (1973).
[20]
Zhang, L., Xiang, Y.: Vibration of open circular cylindrical shells with
intermediate ring supports, Int. J. Solids Struct. 43, 3705–3722 (2006).
[21]
Hotisseini- Hashemi S., Ilkhani M.R.: Identification of the validity range of
Donnell and Sanders shell theories using an exact vibration analysis of
functionally graded thick cylindrical shell panel, Acta Mech. 223, 1101-1118 (2012).
[22]
Aragh B.S., Hedayati H.: Static response and free vibration of two- dimensional
functionally graded metal/ceramic open cylindrical shells under various
boundary conditions. Acta Mech. 223,
309-330 (2012).
[23]
Avramov, K. V.: Nonlinear modes of vibrations for simply
supported cylindrical shell with geometrical nonlinearity, Acta Mech. 223, 279–292 (2012).
[24]
Bolotin V.V.: Vibrations in Mechanics, Vol. 1,
[25]
Vol’mir, A.S.:
[26]
Leissa, A.W.: Vibration of Plates, Washington: National aeronautics and space administration 1969.
[27]
Parker, T.S., Chua, L.O.: Practical Numerical Algorithms for Chaotic Systems,
[28]
Yakubovich, V.A., Starzhinskii, V.M.: Linear Differential Equations with Periodic
Coefficients,
[29]
Guckenheimer, J., Holmes, P.J.: Nonlinear Oscillations, Dynamical Systems and Bifurcations
of Vector Fields,
[30] Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory,
Author addresses:
Department of
Mechanical Engineering,
A.N.
Podgorny Institute for Mechanical Engineering Problems, National Academy of
Sciences of
Fig. 1. Sketch of the
shell
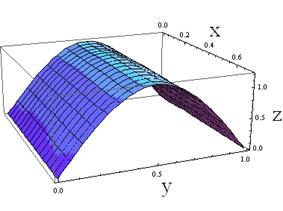
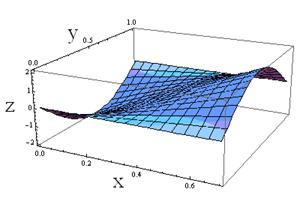
a.
b.
c.
Fig. 2. Three eigenmodes of the shell
linear vibrations with the parameters: a1=1 m, a2=0.7 m, 
m, h=0.01 m; a., b., c. correspond the eigenfrequencies 154.9; 324 and 619.9 (rad/s),
respectively
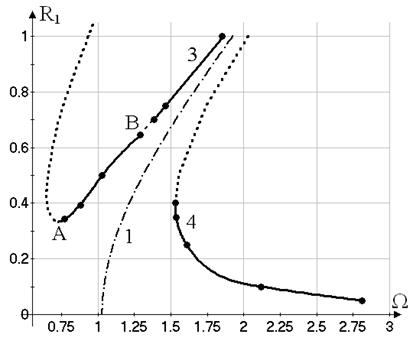
Fig. 3. Backbone curve and frequency responses for the
first generalized coordinate ξ1.
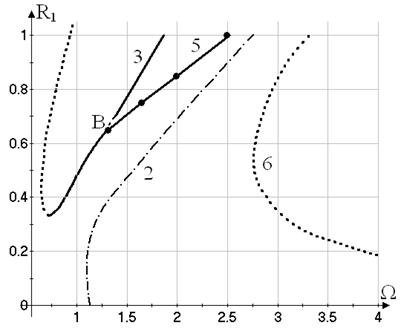
Fig. 4. Backbone curve and frequency responses for the second generalized coordinate ξ2.
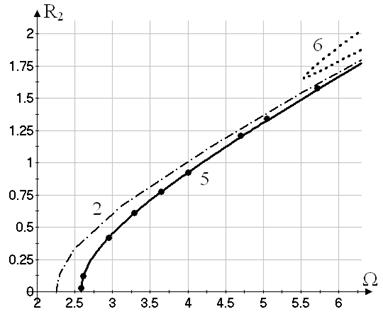
Fig. 5. Backbone
curve and frequency responses for the second generalized coordinate ξ2
Table 1. The dependence of eigenfrequencies on curvature
radius
|
|
n=1 |
n=2 |
n=3 |
|
∞ [24, 28] |
154.9 370.9 1223 |
619.8 915.7 1847 |
1394.7 1722.6 2750.5 |
|
20 |
154.9 369.8 1244.7 |
619.9 909.7 1848.8 |
1394.7 1708.4 2732.9 |
|
5 |
154.9 368.6 1701.6 |
619.9 909.4 2045.7 |
1394.7 1708.3 2795.7 |
|
2.5 |
154.9 366.6 2254.5 |
619.9 908.8 2330.6 |
1394.7 1708.2 2894.8 |
|
1.25 |
154.9 356.7 3981.4 |
619.9 905.3 3401.3 |
1394.7 1706.8 3340.8 |
, Table 2. The dependence of eigenfrequencies on the shell
length
|
|
n=1 |
n=2 |
n=3 |
|
0.3 |
154.9 683.8 2593.8 |
619.9 1476.2 3293.1 |
1394.7 2442.4 4041.3 |
|
0.5 |
154.9 428.1 2558.1 |
619.9 1011.9 2807.5 |
1394.7 1833.8 3451.7 |
|
0.6 |
154.9 366.6 2254.5 |
619.9 908.8 2330.6 |
1394.7 1708.2 2894.8 |
|
0.7 |
154.9 324 2066.6 |
619.9 840.6 1997.6 |
1394.7 1627.9 2530.4 |
|
1 |
154.9 251.9 1701.3 |
619.9 733.9 1393.2 |
1394.8 1508.1 1968.7 |
|
1.5 |
154.9 203.3 1234.9 |
619.9 670.5 964 |
1394.8 1441.3 1648 |
Table 3. The eigenfrequencies, which are obtained by Rayleigh-Ritz method, for the
shell with the following parameters: a1=1
m, a2=0.7
m, m, h=0.01 m
|
N=1 |
n=2 |
n=3 |
|
147.5 309.3 2064 |
598.9 766.1 1948.6 |
1394.7 1614 2588.9 |
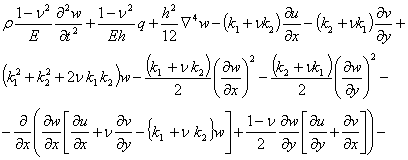
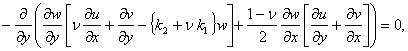
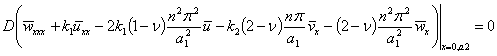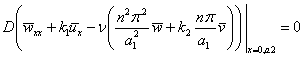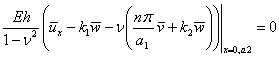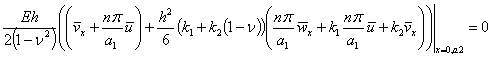